| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
Главная » 2010 » Апрель » 4 » НОВЫЕ ЭКОНОМИЧЕСКИЕ ТЕОРИИ
03:19 НОВЫЕ ЭКОНОМИЧЕСКИЕ ТЕОРИИ |
Но есть другое решение: уничтожать бедность (порождающую ее причину), а не самих бедняков, то есть переводить их в состояние с = 0. Это - человечно, ответственно и эффективно: темпы вырастут до максимума, - убрав, таким образом, отрицательный в (9) вклад состояний < 0, максимально увеличивают еще и крутизну спада функции f( ) при > 0. Математически это означает преобразование распределения доходов Туганова-Цея f(,d,П) с «опасной»МИНИМУМ БЕДНОСТИ, МАКСИМУМ ЭКОНОМИЧЕСКОГО РОСТА – ЭВОЛЮЦИОННО СТАБИЛЬНАЯЯ СТРАТЕГИЯ БЕСКРИЗИСНОГО РАЗВИТИЯ*
Туганов Валерий Федорович, ГНЦ РФ Троицкий институт инновационных и термоядерных исследований, академик МАДЕНМ
«Назвав XXI век веком ответственности, Барак Обама, не сказал главного: как всех освободить от бедности, эксплуатации и кризисов развития, иное - безответственно»
(Алан фон Цей)
«Освобождение Европы придет из России» (Александр Сергеевич Пушкин)
Коротко о главном (вместо предисловия).
«Эволюционно стабильная стратегия (ЭСС), будучи принята большинством, не может быть изменена отклоняющимся индивидуумом или улучшена альтернативной стратегией» (Дж.М. Смит, специалист по теории игр). ЭСС - по определению наилучшая стратегия. Значит, всякая копия чужой ЭСС, - не ЭСС. Вот корни проигрышей России конца XX века: эволюция, движимая конкуренцией и ее борьбой, предпочитает тех, кто выигрывает, - следуя своей ЭСС. Не важно, бизнес это или межстрановые отношения. Разница не велика, главное одно - высокие темпы роста.
Любая общность с рыночной экономикой разделена на два класса , , , , , . Это отверженные: их душевой (в долях среднего) доход не превышает некоторого предела 1 ( 1), а совокупный, как класса, доход не растет даже в растущей экономике. И есть класс избранных: доход каждого из них > 1 и, наоборот, растет, совокупно определяя рост экономики в целом. Бедные, как подкласс отверженных, - в наихудшем положении: их личный (душевой) доход ниже установившегося в общности предела бедности 0 ( < 0< 1) и всегда - даже в растущей экономике - снижается. То есть, отверженные нищают относительно, бедные - абсолютно, доли их в общей численности растут - нестабильность и социальный взрыв неизбежны. Поэтому, имея прямое отношение к ЭСС, здесь существен конкретный ответ: искоренение бедности снижает или повышает экономический рост? Так следует понимать и Л.А. Абалкина, который на Международном симпозиуме по эконофизике и эволюционной экономике (2005 г., Пущино) обозначил эту проблему вопросом: «Почему в растущей экономике возрастает число беднейших слоев?».
Ее и его разрешила физическая кинетика рынка, - создав новое направление физической кинетики.Полученные равновесные функции (вероятности) f( )=f( ,d,П) распределения доходов , будучи функциями дисперсии (коэффициента вариации) доходов d и доли бюджета П в ВВП, глобально задают систему. В частности, определяют и основной закон социофизики: доли отверженных (бедных) растут со снижением d и П. Значит, со снижением дисперсии d эти доли можно стабилизировать, если соответствующим образом повышать П. Это - закон Вагнера (1877 г.), и он давно проявил себя в развитых странах .
Но так ли эволюционирует d? Пусть П, наоборот, неизменно в среднем, число беднейших слоев возрастает тогда, если дисперия d эволюционно снижается со временем. Что и установлено эмпирически при явно большей, чем нуль, средней скорости чистых инвестиций W. Ведь W>0 - растущая (в среднем) экономика. Этот очевидный эмпирический факт, следуя из теории неравновесных откликов функции f( ) (на включение чистых инвестиций), дополняет интегральная зависимость прироста ВВП, но не от функции f( ), а от ее, со знаком минус производной по (см. далее (9)). Отсюда: 1) предел бедности 0 - это наивероятный, максимизирующий распределение f( ) доход; 2) у любого, кто находится в состоянии слева от 0 ( < 0< 1), доход - снижается. Значит, ИСКОРЕНЯЯ БЕДНОСТЬ, можно ПОДНЯТЬ ЭКОНОМИЧЕСКИЙ РОСТ . Достаточно лишь методично «опустошать» все состояния < 0 по мере их появления в распределении f( ). Например, уничтожая (укорачивая жизнь) бедняков. Судя по факту и прогнозу снижения численности населения, этот проект стабилизации роста ВВП, похоже, давно реализован: что с этих лузеров взять, а исключи отрицательный от них вклад - темпы возрастут. Но есть другое решение: уничтожать бедность (порождающую ее причину), а не самих бедняков, то есть переводить их в состояние с = 0. Это - человечно, ответственно и эффективно: темпы вырастут до максимума - убрав таким образом вклад состояний < 0, максимально увеличивают при > 0 крутизну спада функции f( ).
Итак, заложив в исследуемый объект методы физики и выявив суть и законы эволюции, получили необходимое условие эмансипации «либерала» в человека - ЭСС бескризисного развития. Вот ИСТИННАЯ ЛИБЕРАЛЬНАЯ ДЕМОКРАТИЯ: классов нет, а Свобода, Власть и Рынок - для Всех!
«Никто не должен остаться позади!» - это лозунг Великих демократических революций… Значит, - замена «либеральной (в кавычках) демократии» (кризис и бедность тому судья) демократией истинной и истинным либерализмом… Демократия – власть большинства, когда рынок – благо для всех, а не для «избранных». Тогда либерализм – точно так же - свобода для всех: свобода не быть бедным и эксплуатируемым в рынке. А он, - естественно, регулируемый и настроен на оптимум9. Иного, не может быть: нет бедности - нет почвы для финансовых пирамид и кризисов перепроизводства...
1. Поскольку кризис «идет» извне и изнутри, - задача двуединая:
- повышение темпов роста экономики, хотя бы до НЭПовских 20% среднегодовых,
- минимизация бедности и управление этим минимумом.
То есть, минимум бедности, максимум экономического роста.
Минимум бедности очевиден - ее уничтожение и отсутствие. А максимум роста - надо считать: это уж как получится. Бедность, ее рост - эмпирический факт и давно занимающий всех вопрос: «Почему в растущей экономике растет и бедность?». Отсюда и разделение общности на два класса. Если у одних душевой доход ниже некоторого предела и не растет (общий прирост нуль), значит, растет доход остальных. Их общий прирост доходов - рост экономики (совокупного дохода общности). Первые - класс отверженных рынком (с подклассом бедных), вторые - класс избранных.
Но в «свободном», нерегулируемом рынке бедность - это то, чем «кормится» класс избранных: их доход, как показано в , растет не только за счет инвестиций, но и путем перераспределения в свою пользу дохода бедняков. Это и есть эксплуатация человека человеком или - чужого труда. И не надо быть физиком, достаточно хоть краем уха слышать о М.В. Ломоносове: ничто не возникает из ничего, а если прибудет в одном месте, то столько же убудет в другом. Значит, при сравнительно низком росте ВВП - ничего дополнительно к имеющемуся не произведено (почти простое воспроизводство), -если беднеют бедные, богатые богатеют. И власть, и рынок здесь - не для всех: рынок - «ОАО МММ», а власть - «либеральная (в кавычках) демократия».
Власть для всех организует рынок так, что и он - всеобщее благо: доходы растут у всех, хотя и по-разному, - что сродни дивидендам вкладчиков ОАО. Да, неравенство остается: каждый получает доход в соответствии с установившейся иерархией: квалификаций, одаренностей, талантов, призваний и их... признаний общностью. Но никакая «избранная» группа не перераспределяет при этом чужой доход, умаляя его и, тем самым, эксплуатируя чужой труд. Нет классов с разным направлением скорости роста доходов: с минусом для одних, с плюсом для других - все «идут» в одну сторону, хотя и с разной по модулю скоростью. Бессмысленно в этой иерархии винить рынок: у каждого есть лишь повод к собственному продвижению в ней. А это и рост человеческого капитала, и усовершенствование властных и общественных структур, так или иначе, выстаивающих эту иерархию. То есть, все то, что формирует ИЧС – индекс человеческого счастья.
2. Насколько это возможно и почему рынком надо управлять?/center>
Теоретически показано (см. например ), и это согласуется с эмпирическими данными (см. рис.1), что существует закон - основной закон рыночной эволюции. И он существенно меняет сложившиеся представления о свободном развитии рынка и всех, подчиняющихся его законам структур (страна, регион, муниципалитет). Это закон снижения дисперсии (коэффициента вариации) доходов, что, определяя функцию (вероятность) их распределения в каждой общности, задает эволюцию всех ее параметров, а значит, - и общности в целом. Из рис.1 следует, что этой эволюции дисперсии d(t), по крайней мере, качественно, отвечает достаточно простой закон
d(t)/ t - W(t) d(t) (1)
).
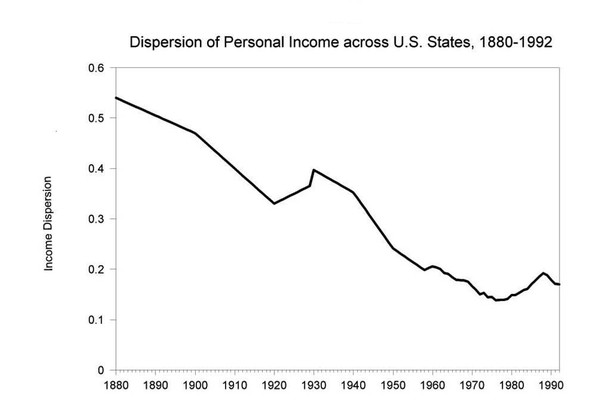
где W(t) - скорость чистых инвестиций в момент времени t. Средняя скорость инвестиций W по большому его интервалу (112 лет) в целом положительна (W>0) - скорость эволюции d(t)/ t<0, и дисперсия d(t) - снижается. Исключение составляют лишь два коротких интервала. Это - начало 20-х до начала 30-х годов (финансовый кризис, предшествующий Великой депрессии и ее начало) и годы «рейганомики» (этим «упражнениям» Рейгана отвечали два существенных кризиса), - где, надо полагать, средние скорости W были отрицательны (W<0), скорость d(t)/ t>0, и дисперсия d(t) - растет (см. рис. 1)
И так как закон - есть закон, то лучше ему подчиниться и, выстроив «по нему» стратегию, - признать, что эволюция дисперсии доходов, а значит, и их распределений, с неизбежностью понуждает заданную ими рыночную систему к постоянному или регулярному управлению.
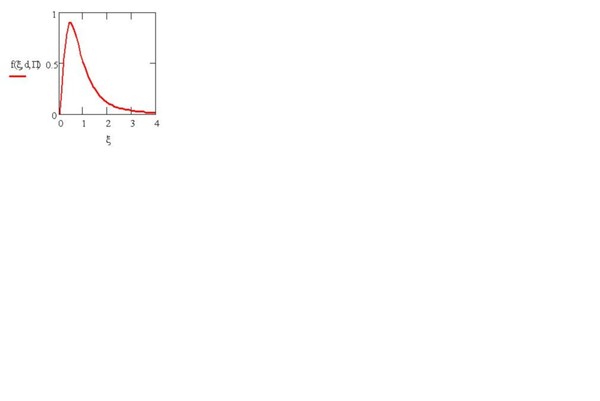
Рис. 2: распределение Туганова-Цея, как функция дохода , дисперсии d и бюджета П (в долях среднего дохода D)
Методы теоретической физики, плюс эмпирика фактов, установленных ведущими исследовательскими группами США, позволили найти и эти функции f()=f(,d,П) (см. рис.2), как функции душевого дохода и двух параметров, где d дисперсия доходов (коэффициент вариации), П – бюджет (все в долях ВВП или общего дохода общности). Достаточно очевиден и ее вид: доли очень бедных и очень богатых в любой общности всегда малы. То есть для крайних значений доходов ( 0 и ) функция f( ) 0. А так как число субъектов общности нулю не равно, то площадь под кривой f( ), определяя его, так же не равна нулю. Значит, f( ) имеет, как минимум, хотя бы один максимум, что отвечает рис. 2. То есть, функция распределения, как бы она ни спадала с ростом дохода, должна быть ограничена еше и при малых доходах. Математически это означает, что интеграл
d f(,d,П) < 2),
определяющий средний доход D должен сходиться. И такое распределение по доходам (распределение Туганова-Цея) было физически предсказано (IV Международная Кондратьевская конференция, 2002 г.) и эмпирически найдено , . Причем, в этих замечательных работах авторы не только получили хорошее согласие с эмпирическими данными целого ряда стран, но и «угадали» форму этих функций. Она достаточно красива
f( ) -1/( + a) -1 + (3)
Но форму надо дополнить содержанием: выяснить смысл параметра a и выявить зависимость коэффициентов a, и от определяющих распределения f(,d,П) параметров d и П. Так и появились распределения (функции) Туганова-Цея, и это тот вклад, что внесли теоретики , , , . Они не только решили эти проблемы (нашли функции a(d,П), (d,П) и (d,П)), но, используя развитые для физики плазмы методы , , , , создали новое направление – физическую кинетику рынка.
Коэффициенты (а,d) и (а,d) зависят от задающего рынок и общность параметра а и коэффициента вариации d= 2/D2, где 2 – дисперсия доходов. Формула (3) определяет более общий закон, нежели чем закон Ципфа-Мандельброта
f( ) 1/( а + ) (4),
который предложил Мандельброт, модифицируя распределение Ципфа. И дело даже не в том, что (4) формально следует из (3) при =1. Все куда глубже: в отличие от (4) коэффициент = (а,d), равно как и =(а,d), являются достаточно сложными функциями параметров d и а. Смысл а не был выяснен до тех пор пока в формуле (3) не проделали два достаточно громоздких предельных перехода по этому параметру. Из (3) было найдено распределение, когда этот фактор существен (а>>1)
f() -1 exp(- ), = (d) 1 (5)
и, наоборот, когда он такой роли не играет (а<<1)
f() exp(-( - 2)/)/ = (d) 3 (6)
А что может быть существенно для беднейших слоев общности? Бюджет! И он же абсолютно не существен для богатых. Поэтому, как минимум,
а = а(d,П) П/(1 - П) (7)
Эти разные экспоненциальные зависимости (5) и (6) были отмечены в (см. стр. 504). Из чего стало ясно: закон (3) - достаточно глубок, причем не только потому, что имеет более общую форму, чем распределение Тсаллиса. Хотя этого достаточно, чтобы при больших значениях дохода () закон снижения вероятности распределения мог иметь не только степенной (6), но и экспоненциальный (5) вид. Но куда важнее, что а имеет отношение к бюджету (см. (7)), точнее к его доле П в ВВП (в совокупном доходе общности): а0 при П0 и а при П1. Именно это и выявляет закон Вагнера (Адольф Генрих Вагнер, 1877) , который давно проявил себя в развитых странах как метод, если не борьбы с бедностью, то хотя бы как один из способов ее стабилизации: с ростом доли бюджета П в ВВП снижается уровень бедности .
Формулы (5)-(6), будучи предельными значениями закона (3) и позволяя выяснить условия применимости каждой из них, оказываются еще и похожими на те, что есть в известном обзоре . С той, правда, разницей, что в распределениях (5)-(6) нет тех «минусов», что присущи аналогичным формулам25. А именно этого достаточно, чтобы признать физическую несостоятельность и формулы (18), и формул (7), (25) в25. Действительно:
1) При стремлении к нулю (d0) коэффициента вариации случайной величины (дохода, например) предложенные в25 вероятности не эволюционируют к дельта-функции Дирака с наивероятным доходом, стремящимся к среднему значению D0. Иными словами, отсутствует зависимость наивероятного дохода 0= 0(d) от дисперсии d, причем 0(d)1 при d0 (или 0(d)/ d<0). А это более чем очевидный (следующий из определения) критерий и известный результат теории вероятностей: при d=0 все доходы, равные друг другу, равны еще и среднему значению. Этому как раз и удовлетворяют формулы (5)-(6): при d0 не только наивероятный доход стремиться к 1, но и функции (5)-(6), равно как и общая для них формула (3), стремятся к дельта-функции Дирака f(,d,П) ( -1).
2) Что до распределения (18) в25, то, будучи зависимым не от дисперсии искомой случайной величины (wealth), а от дисперсии инвестиций (другого, вообще говоря, случайного процесса), оно еще и задано коэффициентами релаксации самого процесса перераспределений. Что получается... Если нет инвестиций, - не будет равновесных распределений? Это не так. К тому же, трудно представить, что распределения вероятностей Максвелла-Больцмана могут зависеть от… частоты столкновений. Нет этого и в формуле (3).
3) К тому же для нахождения формулы (18) в25 закон взаимодействия рыночных субъектов задан так, что все их доходы независимо от начальных условий релаксируют к среднему для всей системы значению, что явно противоречит имеющейся тенденции поляризации доходов. То есть несостоятельна не только «одночастичная» модель рыночных обменов, но и следующая из нее статистическая (кинетическая) модель.
Ко всему этому, следует добавить, что и найденная в формула распределения дохода Старкова, Чернавского, Шербакова точно так же не избежала всех этих трех пунктов, из-за чего ее так же нельзя признать физически состоятельной. Более того, из формулы (16) в26 никоим образом не следует степенное распределение, что явно не отвечает как известным эмпирическим данным (см., например, обзор25), так и формуле (6).
3. Найденные функции распределения доходов важны и интересны сами по себе… В частности, позволяют рассчитать доли бедных o(d,П): их личный доход, будучи ниже предела бедности 0, не растет в растущей экономике. И доли «отверженных» (d,П): их совокупный, как класса, доход не растет при этом – его прирост равен нулю, а душевые доходы ниже некоего предела отверженности 1. Но для расчетов нужно выявить (вычислить) эти предельные значения (0 и 1) душевых доходов , до которых производится интегрирование с функцией распределения f(,d,П)
0(d,П) = d f(,d,П) (d,П) = d f(,d,П) (8) Задача сложная. Однако физику (природу) дохода 0 (и его соотношение с 1) можно выявить из простых рассуждений, показав, что 0=0(d,П) - наивероятный (отвечающий максимуму вероятности распределения f()) доход. Действительно, имеющий с вероятностью f() доход (рис. 2), взаимодействует с теми, чей доход и выше, и ниже его дохода , но, как правило, не намного. В большинстве своем преобладают сделки (покупки) с ценой намного меньшей самого дохода (редко, кто несет в лавку или магазин весь свой доход). Но в любой сделке выигрывает всегда тот, чей душевой доход выше. Поэтому, если твой доход меньше (<0) наивероятного дохода 0, то прирост дохода здесь в среднем отрицателен: наиболее вероятны сделки с имеющими больший, чем твой доход. Для тех, чей доход выше наивероятного (>0), наоборот: прирост дохода положителен, так как более вероятны сделки с обладателями меньших доходов. И лишь при =0 обмены носят эквивалентный характер: ни у кого нет преимуществ.
В отличие от используемых Росстатом логнормальных функций, функции распределения доходов Туганова-Цея f(,d,П) позволяют не только определить абсолютно все статистические данные, но, что не менее важно, - спрогнозировать тенденцию их изменения (эволюции), причем на уровне отдельных территорий (страна, регион, муниципалитет). А это и доли децильных групп, кривые Лоренца, коэффициенты Джини и фондов (неравенства). Включая конкретный расчет «хвостов» распределений доходов - долей и доходов тех, чей доход превышает заданный (что важно для банков, страховых компаний и всякого рода инвесторов, их консультантов и консультантов любого правительства и любого его уровня - муниципалитет, регион, страна, их группа). И, конечно, это расчет доли бедных o(d,П) и доли «отверженных» (d,П) (см. (8)).
Без этих «долей» не обойтись ни политикам, ни тем, кто отвечает за безопасность страны. А для их расчета необходимо выявить (вычислить) соответствующие предельные значения (0 и 1) душевых доходов , до которых производится суммирование по числу субъектов, а точнее, - интегрирование по с известной функцией (вероятностью) распределения Туганова-Цея f(,d,П). Само же уравнение, определяющее, например, предельный доход 1=1(d,П) для доли «отверженных» (d,П), задано условием, когда их совокупный прирост дохода равен нулю. Поэтому, теми же методами на основе найденных кинетических уравнений исследован и отклик этих функций на воздействие инвестиций – чистых инвестиций (капитала) с заданной скоростью их среднего роста W. И в линейном по W приближении, в частности, вычислены соответствующие к этим функциям распределения добавки, которые определяют не только перераспределения доходов при инвестировании, но и эволюцию (закон изменения) самих параметров системы.
Так и был получен закон, определяющий средние темпы роста ВВП при инвестировании, который на временах t>>1/ R имеет вид
(d,П) = W/ d /R(d,П,)(- f(,d,П)/ ) (9)
напоминающий закон Ома (самый известный пример отклика системы на внешнее воздействие). Здесь - скорость внутренних инвестиций, а R=R(d,П,) – сопротивление инвестициям, которое аналогично сопротивлению среды при протекании тока ((d,П) в (9) ) при заданном напряжении ( W/ в (9) ). Зависимость левой части (9) от d и П результат того, что средние темпы роста (d,П) определяются суммированием по всем субъектам, точнее, - интегралом по с известной функцией распределения f(,d,П).
Итак, конкуренция, в том числе и межстрановая, понуждает субъекта к увеличению скорости роста капитала (чистых инвестиций) W. Тогда, в соответствии с (9) возрастает отклик (d,П) - прирост ВВП (общего дохода общности): с большей скоростью инвестируешь, больше, при прочих равных условиях, получишь. Так и оказывается: какие бы катаклизмы локально по времени ни происходили, средняя скорость инвестиций W по большому его интервалу - положительна (на что и указывают рис. 1 и формула (1)).
То есть, формируя в рыночной системе среднюю скорость инвестиций W>0, конкуренция задает и экономический рост, и снижение дисперсии доходов d как основной закон эволюции, d(t) 0 (см. формулы (1) и (9)). Отсюда - основной закон социофизики:
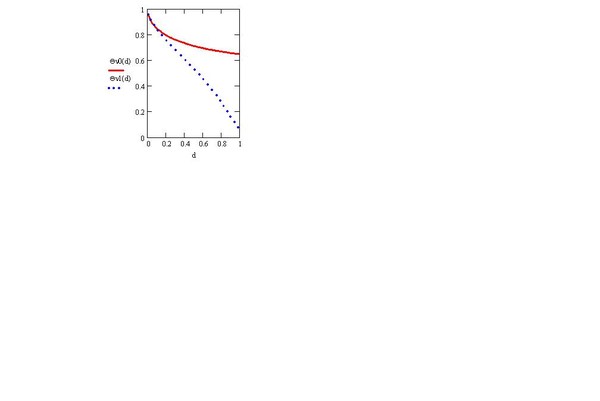
Рис. 3: предельные (универсальные) кривые: 0(d)=(d,0) (сплошная линия) и 1(d)=(d,1) (пунктир), между которыми находится доля отверженных (d,П) при любом из значений 0<П<1 бюджета П.
доли отверженных (бедных) растут со снижением d и П (см. рис. 3). Значит, со снижением дисперсии d, эти доли можно стабилизировать, если соответствующим образом повышать П. Это - закон Вагнера (1877 г.), и он давно проявил себя в развитых странах.
На. рис. 3 доля (d,П) как функция d находится при любом из значений 0<П<1 бюджета П между двумя предельными (универсальными) кривыми: 0(d)=(d,0) (сплошная линия) и 1(d)=(d,1) (пунктир). Значит, где бы, в каких бы условиях (при , d и П) ни находилась общность, будучи «зажатой» этими предельными (для 0<П<1) кривыми, она с вероятностью 1 придет в силу закона эволюции (d 0) к состоянию с =1 (если такую 100%-ую «отверженность» допустит народ). Что, в конце концов, и приводит общность к краху закона Вагнера: начиная с некоторого, критического значения дисперсии dcr (dcr) перестает зависеть от П. Физическая причина, порождая социально-экономическую неуправляемость, собственно и есть причина революционной ситуации: «верхи не могут управлять по старому», а «низы не хотят по-старому жить» . И не зная как «управлять по-новому», верхи собственно и доводят ситуацию до логического конца…
И все исключительно из-за роста численности (доли) беднейших слоев (см. рис. 3). А природа этой бедности не только в том, что есть люди (доля их равна 0, см. (8)), доходы которых предельно низки - ниже наивероятного дохода 0, но здесь (0<<0) еще и производная функции распределения положительна ( f()/ >0). Поэтому даже в растущей экономике личные их доходы – всегда снижаются, и вклад их в общий прирост (9) – отрицательный (см. рис. 3). То есть равный нулю совокупный прирост доходов возможен лишь с включением в класс бедных еще и части тех, чьи доходы (0<<1) растут, начиная с >0, а достигнув предела 1, полностью компенсируют до нуля общий при 0<<1 спад доходов. Так и формируется класс отверженных (рынком и общностью): душевые их доходы <1, а общий, как класса, доход – не растет даже в растущей экономике. Значит, в условиях неуправляемого рынка весь прирост общего дохода общности обусловлен ростом дохода избранных: тех, чьи доходы 1>0, где производная функции распределения f()/ <0 (см. (9)).
В класс «отверженных», таким образом, и попадает средний класс (0<<1), который в марксовом понимании группируется, начиная с наивероятного дохода 0. Отсюда вся революционность среднего класса, о гегемонии которого в «неотвратимо» предстоящей революции заявляют контр-адмирал К. Пэрри и эксперты возглавляемого им военного «мозгового» центра Великобритании (www.mod.uk/DCDC) , .
Насколько предопределена эта революция? И можно ли управлять этим процессом?
4. Итак, для 100%-ной эквивалентности обменов необходимо, чтобы функция распределения доходов f() всюду, на всем интервале душевых доходов общности (0<< ) была постоянна, f()=const. Что невозможно в принципе, исходя из формы и вида этой функции (рис. 2). И, тем более, невозможно - в растущей экономике: для ее роста необходима область доходов с отрицательной производной f()/ <0 (см. (9)). Но такая форма f(), с разными знаками ее производной, составляя суть (физику) неэквивалентности рыночных обменов, собственно и ведет к формированию двух, физически выделенных и заведомо разных классов. Это избранные рынком и им отверженные: в растущей (инвестируемой) экономике доходы первых растут, у вторых - совокупный прирост дохода равен нулю. Отверженные нищают относительно, бедные - абсолютно, причем доли их в общей численности эволюционно растут - нестабильность и социальный взрыв неизбежны. Физическая экономия (физическая кинетика рынка), выявив общую природу неэквивалентности рыночных обменов, существенно дополняет здесь марксову теорию, расширяя ее на весь спектр отношений.
Именно такие обмены, формируя бедность и ее численность (расчеты дают 0 25%, 60%), эволюционно ведут к их росту. И закон Вагнера (повышение доли бюджета П в ВВП) – всего лишь временная мера… Значит, задача в том, чтобы привести общность к состоянию, где доля (степень) бедности заведомо равна нулю (0(d,П)=0).
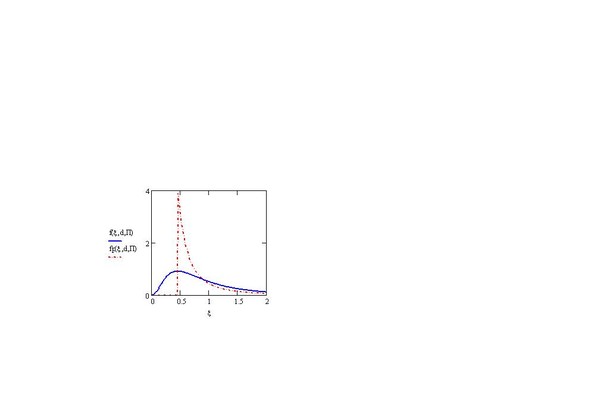
Рис. 4: преобразование распределения доходов Туганова-Цея f(,d,П) (сплошная кривая) в распределение Парето (пунктир)
Для этого достаточно лишь методично «опустошать» все состояния < 0 по мере их появления в распределении доходов общности f( ). Например, уничтожая (укорачивая жизнь) бедняков. Судя по факту и прогнозу снижения численности населения, этот «неолиберальный» проект стабилизации роста ВВП, похоже, давно реализован: что с этих лузеров взять, а исключи отрицательный от них вклад в (9) - темпы возрастут. Но есть другое решение: уничтожать бедность (порождающую ее причину), а не самих бедняков, то есть переводить их в состояние с = 0. Это - человечно, ответственно и эффективно: темпы вырастут до максимума, - убрав, таким образом, отрицательный в (9) вклад состояний < 0, максимально увеличивают еще и крутизну спада функции f( ) при > 0. Математически это означает преобразование распределения доходов Туганова-Цея f(,d,П) с «опасной» областью доходов (0<<0) - (сплошная кривая на рис. 4) - в распределение Парето, не обладающее таким свойством. Его функция fp(,d,П) вообще не имеет области низких доходов: fp(,d,П)=0 при <0. А, начиная с 0, с ростом дохода вероятность fp(,d,П) его иметь – снижается: спадает степенным образом от максимального при =0 значения (на рис. 4 – пунктир). Необходимый для этого налог должен быть прогрессивным: отрицательным для бедных (<0) и положительным для остальных (>0). Все это позволит выявить не только степень этой прогрессии, но и ответ на главный вопрос: сколько всего средств надо перераспределить? Столько, чтобы довести доход каждого бедняка до минимального уровня 0 .
H = H(d,П ) = d (0 - ) f(,d,П) (10)Сегодня это 4% (H=3.7%) - половина среднегодового прироста ВВП (порядка 7%). Однако, если учесть, что такая трансформация распределения доходов увеличивает темпы роста ВВП - примерно в 3-3.5 раза, то эти 4% не покажутся и цифрой: нынешние 7% 3.5 24%, минус эти 4% и издержки по поддержанию распределения доходов в виде Парето-распределения fp(,d,П), - все это и есть те легендарные и никем непревзойденные 20% среднегодового роста при НЭПе .
5. Вот истинная цена свободы - цена истинной либеральной демократии. Здесь рынок - благо для всех. И все истинно свободны: от бедности, эксплуатации человека человеком и кризисов в развитии.
Ответ за властью: готова ли она, заявив об ответственности, стать благом для всех? Недавно президент России Д.А Медведев заявил, что к 2010 г. в России не будет пенсионеров с пенсией ниже 8 тыс. руб. На Байкальском экономическом форуме его поддержал и министр финансов А. Кудрин: пенсии будут доведены до прожиточного минимума. Но это означает, что и сам этот уровень должен быть равен 8 тыс. руб.
Вопросов здесь сразу несколько… Верна ли эта цифра? Развиваемая теория (технология) определяет прожиточный минимум доходом, при котором распределение (вероятность) доходов имеет максимум (рис. 2). Это - наивероятный доход
D0(d,П) = 0(d,П) D(d,П) (11),
где D(d,П) – средний доход общности. Для любой общности (территории) все это физически измеримо, а значит, бесспорно (никому не покажется несправедливым): D(d,П) и 0(d,П) измеряются и вычисляется с использованием статистических данных. В среднем по всей России 0(d,П) 0.5, а D(d,П) 16 тыс. руб. (официальные данные). То есть в среднем, действительно D0(d,П) 8 тыс. руб.
Но основной результат теории носит комплексный характер: если прожиточный минимум на какой-то территории (страна, регион) определить наивероятным доходом, то это не только искоренит бедность (не будет тех, чей доход снижается даже в растущей экономике), но и-и-и…. УВЕЛИЧИТ здесь темпы роста! Очевидно, если темпы вырастут в каждом регионе (муниципалитете), они вырастут и во всей стране (в каждом регионе). Однако наивероятный доход, как и средний доход на каждой территории - РАЗНЫЕ. Поэтому разным должен быть и прожиточный минимум – для каждой территории свой.
Если же работать со средним по России значением в 8 тыс. руб. – эффекта в целом не будет: ни по искоренению бедности, ни с повышением темпов экономического роста. Значит, задача в том, чтобы, как минимум, ежегодно, достаточно быстро (в течение короткого времени исследований) произвести расчет около 200 параметров: почти 90 субъектов, плюс их столицы и еще порядка 20 субъектов особого подчинения. Технически и технологически справиться с этим можно лишь на основе расчетов и методик, предлагаемых в данной работе.
Выводы:
1) Уничтожение бедности не только и не столько нравственная проблема общности, - это вопрос ответственности власти, а, стало быть, - эффективности и правильности управления: «управлять – поступать правильно, кто тогда посмеет неправильно поступать» .
2) Технологически и методологически проблема эффективности управления решена: наука вместо воинствующего суеверия «демократий» - ЭСС не возникают из процедур голосования, разветвления властей и предвыборных «пиар-упражнений». Тем более, что «чужих» ЭСС – не бывает: любая копия ЭСС – не ЭСС.
3) Все должны прекрасно понимать: «плохие дороги не ведут к храму: либо это не Храм, либо не та Дорога»33. Вот ИСТИННАЯ ЛИБЕРАЛЬНАЯ ДЕМОКРАТИЯ: классов нет, а Свобода, Власть и Рынок - для Всех!
P.S. Физически задача ставится иначе: кинетические уравнения для функций fp(,d,П) должны быть дополнены соответствующими потоками доходов. А так как сами функции выявлены (из физических соображений), то найденные потоки следует сопоставлять с возможностями налогообложения. Значит, вся юриспруденция и Закон следуют не из борьбы «народных избранников», лоббирующих интересы разных классов и групп, а из Физики (Природы) налогообложения. Оно - бесспорно прогрессивное, а степень этой прогрессии задана самой природой (сутью) решаемых проблем.
Туганов В.Ф. Минимум бедности, максимум экономического роста - эволюционно стабильная стратегия бескризисного развития. V Всероссийская научно-практическая конференция «Научное, экспертно-аналитическое и информационное обеспечение национального стратегического проектирования, инновационного и технологического развития России», 2009, 28-29 мая, Москва, ИНИОН РАН. Сб. научных трудов, ч. 1, С. 491-497
Литература
* Работа выполнена при поддержке Международного научного фонда экономических исследований академика Н.П. Федоренко, проект № 2008-096
1. Туганов В.Ф. (2005): Физика коммунитаризма: управление рынком и эволюционно стабильная стратегия (ЭСС) развития. Сборник трудов IV Всероссийской интернет–конференции по проблемам эконофизики и эволюционной экономики. Екатеринбург, 21–30 ноября. www.ephes.ru.
2. Туганов В.Ф., Туганов И.В. (2006): Рынок и коммунитарное (частно–государственное) партнерство: как справедливо разделить пирог ВВП и почему необходимо управлять рынком? http://spkurdyumov.narod.>ru
3 Туганов В.Ф. (2007): Физическая кинетика рынка: ВВП, его «удвоение» и борьба с неравенством и бедностью. Эконофизика. Современная физика в поисках экономической теории. М.: МИФИ.
4 Туганов B.Ф. (2007): Физическая кинетика рынка: либерализм, коммунитарность, коммунизм – к чему эволюционируем? Сборник трудов VI Всероссийской Интернет–конференции по проблемам эконофизики и эволюционной экономики. Екатеринбург, 16–30 апреля. www.ephes.ru
5 Туганов В.Ф, Туганов И.В. (2008). Простая модель рынка: экономический рост, богатство и бедность. Львовские чтения. Сборник научных трудов по материалам конференции Государственный университет управления. М.: ГУУ, с. 152-155
6 Туганов В.Ф. (2007): Физическая кинетика рынка: ВВП, его «удвоение» и борьба с неравенством и бедностью. Эконофизика. Современная физика в поисках экономической теории. М.: МИФИ.
Туганов В.Ф. (2008). Физическая кинетика рынка: социальна ли политика государства? Экономика и математические методы, т. 44, № 1
8 Туганов В.Ф. (2008). Физическая кинетика рынка: основной закон рыночной эволюции и стратегия управления развитием. Сборник докладов на конференции лауреатов Международного научного фонда экономических исследований академика Н.П. Федоренко (в печати)
9. Туганов В.Ф, Туганов И.В. (2008). Простая модель рынка: экономический рост, богатство и бедность. Львовские чтения. Сборник научных трудов по материалам конференции Государственный университет управления. М.: ГУУ, с. 152-155
10. Туганов В.Ф., Туганов И.В. (2006): Рынок и коммунитарное (частно–государственное) партнерство: как справедливо разделить пирог ВВП и почему необходимо управлять рынком? http://spkurdyumov.narod.>ru
11. Xavier Sala-i-Martin (2005): The World Distribution of Income: Falling Poverty and… Convergence, Period. IncomDistrAnimation_DRAFT>_030924. www.nber.org.
12. Scafetta N., Picozzi S., West B.J. (2004): An Out-of-equilibrium Model of the Distributions of Wealth // Quantitative Finance. № 4. P. 353–364.
13. Scafetta N., Picozzi S., West B.J. (2002): Pareto’s Law: a Model of Human Sharing and Creativity // arXiv: cond-mat/0209373. Vol. 1. 16 sep.
14. Туганов В.Ф. (2005): Физика коммунитаризма: управление рынком и эволюционно стабильная стратегия (ЭСС) развития. Сборник трудов IV Всероссийской интернет–конференции по проблемам эконофизики и эволюционной экономики. Екатеринбург, 21–30 ноября. www.ephes.ru.
15. Туганов В.Ф. (2005): Вперед к природе: физика налогообложения, демократии и управления развитием. Круглый стол «Проблемы законодательного регулирования и государственной политики по развитию нанотехнологий в РФ», Совет Федерации, 31 марта.
16. Туганов В.Ф., Туганов И.В. (2005): Управление рынком и эволюционно стабильная стратегия (ЭСС) развития. III Международная конференция «Развитие регионов России и укрепление сотрудничества России со странами Европейского Союза». 19 октября. М.: НКЭР. www. nker.
17. Туганов В.Ф. (2007): Физическая кинетика рынка: ВВП, его «удвоение» и борьба с неравенством и бедностью. Эконофизика. Современная физика в поисках экономической теории. М.: МИФИ.
18. Туганов В.Ф. Препринт ГНЦ РФ ТРИНИТИ N 0096-А (26.02.2002).
19. Туганов В.Ф. Тезисы докладов XXIX Звенигородской конференции по физике плазмы и УТС, 25.02-01.03.2002.
20. Туганов В.Ф. Тезисы докладов XVIII конференции по Фундаментальной Атомной Спектроскопии (ФАС - XVIII), Научный совет РАН по спектроскопии атомов и молекул, г. Звенигород, 22-26 октября 2007.
21. Tuganov V.F. On the Langmuir waves absorption in plasma. Landau damping and the collisions role. The subject of the International Conference MSS-09 "Mode Conversion, Coherent Structures and Turbulence" (2009)
22. Туганов В.Ф. (2007): Физическая кинетика рынка: ВВП, его «удвоение» и борьба с неравенством и бедностью. Эконофизика. Современная физика в поисках экономической теории. М.: МИФИ.
23. Wagner A.H. (1877, 1890): Finanzwissenschaft. Vol. I, II. Leipzig: C.F. Winter.
24. Туганов В.Ф. (2008). Физическая кинетика рынка: социальна ли политика государства? Эконо
|
|
Категория: Новости |
Просмотров: 358 |
Добавил: muchought
| Рейтинг: 0.0/0 |
|
|





